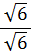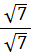Rationalising Surds
Rationalise surds means multiplying the top and bottom of a fraction by a surd so that the resulting number has the surd on the numerator and not the denominator. It can also be called rationalising the denominator as this process changes the denominator from an irrational number (a surd) to a rational number.
| • | Example 1. | Rationalise the denominator of | 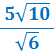 |
| (a) multiply top and bottom by √6 | ||||||
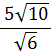 | = |
| ||||
| (b) note √6 × √6 = 6 | ||||||
| = | 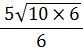 | |||||
| = | 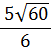 | |||||
| (c) 4 is both a factor of 60 and a perfect square | ||||||
| = | 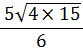 | |||||
| = | 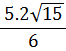 | |||||
| = | 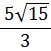 | |||||
| • | Example 2. | Rationalise the surd | 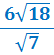 |
| (a) multiply top and bottom by √7 | ||||||
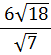 | = |
| ||||
| (b) note √7 × √7 = 7 | ||||||
| = | 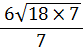 | |||||
| = | 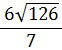 | |||||
| (c) 9 is both a factor of 126 and a perfect square | ||||||
| = | 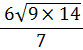 | |||||
| = | 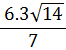 | |||||
| = | 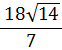 | |||||