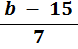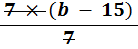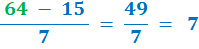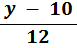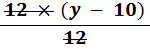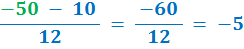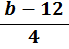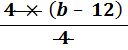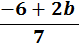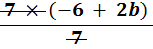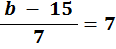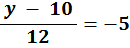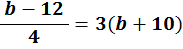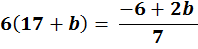
Answers − Solving Equations 2

1.   If 42 + y = 20 + 3y     solve y

i. Subtract 20 from both sides

		42	+	y	=		20	+	3y
	−	20			=	−	20

22

+

y

=

+

3y

ii. Move y to one side. So subtract y from both sides

		22	+	y	=		+	3y
			−	y	=		−	y

22

=

2y

iii. Divide both sides by 2

		22		=			2y
	÷	2		=		÷	2

11

=

y

iv. To verify, put the value of y = 11 back into the original equation:

both sides are equal

2.   If 6 + 4b = 15 + b     solve b

i. Subtract 6 from both sides

		6	+	4b	=		15	+	b
	−	6			=	−	6

+

4b

=

9

+

b

ii. Move b to one side. So subtract b from both sides

		+	4b	=		9	+	b
		−	b	=			−	b

3b

=

9

iii. Divide both sides by 3

		3b	=			9
	÷	3	=		÷	3

b

=

3

iv. To check, put the value of b = 3 back into the original equation:

both sides are equal

3.   If 37 + t = 2(26 + 3t)     what is the value of t?

i. Multiply the brackets on RHS

37

+

t

=

2(26

+

3t)

37

+

t

=

52

+

6t

ii. Subtract 52 from both sides

		37	+	t	=		52	+	6t
	−	52			=	−	52

−

15

+

t

=

6t

iii. Move t to one side. So subtract t from both sides

	−	15	+	t	=				6t
			−	t	=			−	t

−

15

=

5t

iv. Divide both sides by 5

	−	15		=			5t
	÷	5		=		÷	5

−

3

=

t

v. To verify, put the value of t = −3 back into the original equation:

both sides are equal

4.   If 2(9 + y) = 4(7 + 3y)     what is the value of y?

i. Multiply the brackets on LHS and RHS

2(9

+

y)

=

4(7

+

3y)

18

+

2y

=

28

+

12y

ii. Subtract 28 from both sides

		18	+	2y	=		28	+	12y
	−	28			=	−	28

−

10

+

2y

=

12y

iii. Move 2y to one side. So subtract 2y from both sides

	−	10	+	2y	=				12y
			−	2y	=			−	2y

−

10

=

10y

iv. Divide both sides by 10

	−	10		=			10y
	÷	10		=		÷	10

−

1

=

y

iv. To check, put the value of y = −1 back into the original equation:

both sides are equal

5.   If 3(y − 120) = 5(y + 30)     what is the value of y?

i. Multiply the brackets on LHS and RHS

3(y

−

120)

=

5(y

+

30)

3y

−

360

=

5y

+

150

ii. Subtract 150 from both sides

		3y	−	360		=		5y	+	150
			−	150		=			−	150

3y

−

510

=

5y

iii. Move 3y to one side. So subtract 3y from both sides

		3y	−	510		=		5y
	−	3y				=	−	3y

−

510

=

2y

iv. Divide both sides by 2

	−	510		=		2y
	÷	2		=	÷	2

−

255

=

y

v. To verify, put the value of y = −255 back into the original equation:

both sides are equal

6.

If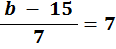

what is the value of b?

i. Multiply both sides by 7

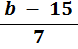			=	7
	× 7		=	× 7

=

49

b − 15

=

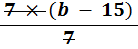49

ii. Add 15 to both sides

		b − 15	=	49
		+ 15	=	+15

b

=

64

iii. To check, put the value of b = 64 back into the original equation:

    

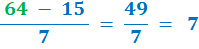
7.

If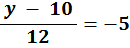

what is the value of y?

i. Multiply both sides by 12

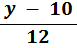			=	−5
		× 12	=	× 12

=

−60

y − 10

=

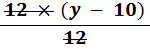−60

ii. Add 10 to both sides

		y − 10	=	−60
		+ 10	=	+10

y

=

−50

iii. To verify, put the value of y = −50 back into the original equation:

    

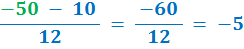
8.

If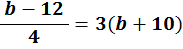

what is the value of b?

i. Multiply both sides by 4

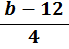			=	3(b + 10)
		× 4	=	× 4

=

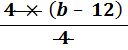12(b + 10)

b

−

12

=

12b

+

120

ii. Subtract 120 from both sides

		b	−	12	=	12b	+	120
			−	120	=		−	120

b

−

132

=

12b

iii. Subtract b from both sides

		b	−	132	=	12b
	−	b			=	−b

−

132

=

11b

iv. Divide both sides by 11

		−	132	=	11b
		÷	11	=	÷11

−12

=

b

v. To check, put the value of b = −12 back into the original equation:

both sides are equal

9.

If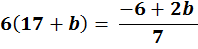

what is the value of b?

i. Multiply both sides by 7

	6(17 + b)	=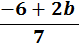
	× 7	=	× 7

42(17 + b)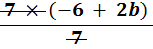

=

714

+

42b

=

−6

+

2b

ii. Subtract 714 from both sides

		714	+	42b	=	−6	+	2b
	−	714			=	−714

42b

=

−

720

+

2b

iii. Subtract 2b from both sides

		42b	=	−	720	+	2b
	−	2b	=			−	2b

40b

=

−

720

iv. Divide both sides by 40

		40b	=	−	720
	÷	40	=	÷	40

b

=

−18

v. To verify, put the value of b = −18 back into the original equation:

both sides are equal

         back to: